10212. Almost shortest path – weighted
Finding the shortest path
that goes from a starting point to a destination point given a set of points
and route lengths connecting them is an already well known problem, and it’s even
part of our daily lives, as shortest path programs are widely available
nowadays.
Most people usually like
very much these applications as they make their lives easier. Well, maybe not
that much easier.
Now that almost everyone can
have access to GPS navigation devices able to calculate shortest paths, most
routes that form the shortest path are getting slower because of heavy traffic.
As most people try to follow the same path, it's not worth it anymore to follow
these directions.
With this in his mind, your
boss asks you to develop a new application that only he will have access to,
thus saving him time whenever he has a meeting or any urgent event. He asks you
that the program must answer not the shortest path, but the almost shortest
path. He defines the almost shortest path as the shortest path that goes from a
starting point to a destination point such that no route between two
consecutive points belongs to any shortest path from the starting point to the
destination.
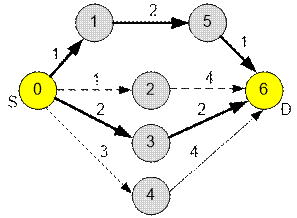
For example, suppose the
figure below represents the map given, with circles representing location
points, and lines representing direct, one-way routes with lengths indicated.
The starting point is marked as s and
the destination point is marked as d.
The bold lines belong to a shortest path (in this case there are two shortest
paths, each with total length 4). Thus, the almost shortest path would be
the one indicated by dashed lines (total length 5), as no route between
two consecutive points belongs to any shortest path. Notice that there could
exist more than one possible answer, for instance if the route with
length 3 had length 1. There could exist no possible answer as
well.
Input. Contains several test cases.
The first line of a test case contains two integers n (2 ≤ n ≤ 500)
and m (1 ≤ m ≤ 104), indicating respectively the number of
points in the map and the number of existing one-way routes connecting two
points directly. Each point is identified by an integer
between 0 and n – 1.
The second line contains two integers s
and d, indicating respectively the
starting and the destination points (s
≠ d; 0 ≤ s, d
< n).
Each one of the
following m lines contains three integers u, v è p (u ≠ v, 0 ≤ u, v < n, 1 ≤ p ≤ 103), indicating the existence of a one-way route from u to v with
distance p. There is at most one
route from a given point u to
a given point v, but notice that the
existence of a route from u to v does not imply there is a route
from v to u, and, if such road exists, it can have a different length. The
last line contains two zeros and will not be processed.
Output. For each test case print a
single line, containing -1 if it is not possible to match the
requirements, or an integer representing the length of the almost shortest path
found.
|
Sample input |
Sample output |
|
7 9 0 6 0 1 1 0 2 1 0 3 2 0 4 3 1 5 2 2 6 4 3 6 2 4 6 4 5 6 1 4 6 0 2 0 1 1 1 2 1 1 3 1 3 2 1 2 0 3 3 0 2 6 8 0 1 0 1 1 0 2 2 0 3 3 2 5 3 3 4 2 4 1 1 5 1 1 3 0 1 0 0 |
5 -1 6 |
SOLUTION
graphs – Dijkstra
Algorithm analysis
A directed weighted graph with two
vertices s and t is given. Let the value of the shortest path from s to t
be d. An almost shortest path from s
to t is a path of least cost that
does not pass along any edge along which a path of length d can pass. In the problem, you should find the length of the almost shortest path or output -1 if
such a path does not exist.
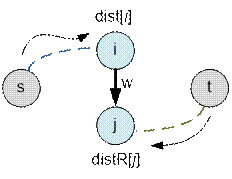
Run Dijkstra’s algorithm from vertex s on a given graph and from vertex t on the reversed graph. Construct two
arrays dist and distR (dist Reverse), where
·
dist[i] is
equal to the length of the shortest path from s to i on the original graph;
·
distR[j] is equal to
the length of the shortest path from t to j on the reversed graph;
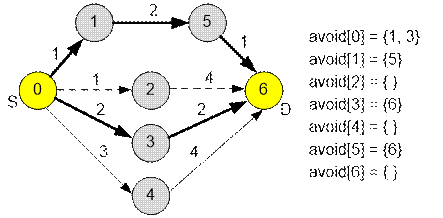
All edges that can lie on the shortest
path should be stored in array of sets avoid:
avoid[i] contains such a set of
vertices j that the shortest path can
pass through an edge (i, j) of length w. This is possible only if the equality holds:
dist[i] + w +
distR[j] == dist[t]
It remains to run Dijkstra’s algorithm one
more time along the edges that are not included in avoid. The path found will be the
almost shortest. Its length will be strictly greater than d.
Algorithm realization
Declare
the constants and arrays.
#define MAX 502
#define INF 0x3F3F3F3F
int used[MAX], parent[MAX];
vector<set<int> > avoid;
Declare
the structure of the edge:
·
node – the number of the vertex where the edge enters;
·
dist – the length of the edge;
struct edge
{
int node, dist;
edge(int node, int dist) : node(node), dist(dist) {}
};
Function to compare the edges. Sort the edges in ascending order of their lengths.
bool operator< (edge a, edge b)
{
return a.dist > b.dist;
}
The input graph is stored in the adjacency list g. The reversed graph (edges are oriented in the opposite
direction) is stored in the adjacency list gr.
vector<vector<edge> > g, gr;
vector<int> dist, distR;
The edges connecting the starting vertex to v are stored in the
vector of sets avoid. avoid[i] contains such a set of vertices j that the shortest path can pass through the edge (i, j).
void path(int v)
{
if (parent[v] == -1) return;
avoid[parent[v]].insert(v);
path(parent[v]);
}
Function Dijkstra implements Dijkstra’s algorithm. It is passed
the adjacency list of the graph g,
the array of shortest distances dist,
the starting s and the final f vertices.
int Dijkstra(vector<vector<edge> > &g, vector<int> &dist, int s, int f)
{
Initialize the
array of shortest distances dist.
dist = vector<int>(n, INF);
dist[s] = 0;
Initialize the
parent array parent (we’ll use it to restore the path from the
start vertex to the
given vertex). Declare all
vertices not processed: used[i] = 0.
memset(parent, -1, sizeof(parent));
memset(used, 0, sizeof(used));
Declare a
priority queue pq. Insert to it the starting
vertex s, the shortest distance to which is 0.
priority_queue<edge> pq;
pq.push(edge(s, 0));
while (!pq.empty())
{
Extract the pair e
from the priority queue pq. The e.node value stores
the number of the current vertex, e.dist contains the
distance from the starting vertex s to e.node.
edge e = pq.top(); pq.pop();
int v = e.node;
If the shortest distance to the final f is already computed, then finish the algorithm.
if (v == f) return dist[f];
If the
vertex v = e.node is a fictive (the
distance e.dist from start s is greater than the already computed value dist[v]), then skip it.
if (e.dist > dist[v]) continue;
Iterate
the vertices, adjacent
to v.
for (int i = 0; i < g[v].size(); i++)
{
Consider
an edge (v,
to) of length cost.
int to = g[v][i].node;
int cost = g[v][i].dist;
If the
edge (v,
to) belongs to avoid, do not consider it.
if (avoid[v].find(to) != avoid[v].end()) continue;
If the vertex to is not yet
included in the set of vertices, the shortest distance to which is already computed (used[to] = 0), then relax the edge (v,
to).
if (!used[to] && dist[to] > dist[v] + cost) // Relaxation
{
dist[to] = dist[v] + cost;
pq.push(edge(to, dist[to]));
parent[to] = v;
}
}
}
We didn’t
reach the final vertex f, return -1.
return -1;
}
The main part of the program. Read the input data.
while (scanf("%d %d", &n, &m), n + m)
{
scanf("%d %d", &s,
&f);
g.clear(); g.resize(n);
gr.clear(); gr.resize(n);
avoid.clear(); avoid.resize(n);
Construct
the graph g. Construct the reversed graph gr.
for (i = 0; i < m; i++)
{
scanf("%d %d %d", &b,
&e, &w);
g[b].push_back(edge(e, w));
gr[e].push_back(edge(b, w));
}
Run the Dijkstra algorithm from the vertex s. Fill the array of
shortest distances dist.
d = Dijkstra(g, dist, s, f);
Run the Dijkstra algorithm from the vertex f along the edges of the reversed graph. Fill the array of shortest distances distR.
d = Dijkstra(gr, distR, f, s);
Iterate over
the edges of the graph
(u, v). Those of them that lie on at least
one shortest path are stored in avoid.
for (u = 0; u < g.size(); u++)
{
for (i = 0; i < g[u].size(); i++)
{
v = g[u][i].node;
w = g[u][i].dist;
if (dist[u] + w + distR[v] == dist[f]) avoid[u].insert(v);
}
}
Run the Dijkstra algorithm from the vertex s. Since the array
avoid is no longer empty, we look for an almost shortest path – a path that does not go through any edge of the shortest
path.
d = Dijkstra(g, dist, s, f);
Print the length of
the almost shortest path.
printf("%d\n", d);
}